Triangles congruence proofs booklet answer key – The Triangle Congruence Proofs Booklet Answer Key unlocks the mysteries of triangle congruence, providing a comprehensive guide to the theorems and proofs that establish the equality of triangles. This booklet empowers learners with the knowledge and skills to navigate the intricacies of geometric reasoning, fostering a deeper understanding of triangle properties and relationships.
Through a systematic approach, the booklet presents the Side-Side-Side (SSS), Side-Angle-Side (SAS), and Angle-Side-Angle (ASA) Congruence Theorems, laying the foundation for proving triangle congruence. Each theorem is meticulously explained, followed by detailed examples that illustrate their application in real-world scenarios.
Congruence Theorems
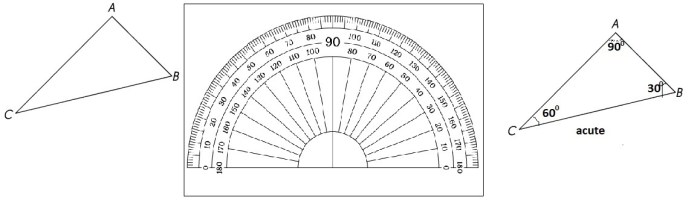
Congruence theorems are geometric principles that establish conditions under which two triangles can be proven to be congruent. These theorems provide a foundation for understanding and solving problems related to triangle congruence.
Side-Side-Side (SSS) Congruence Theorem
The SSS Congruence Theorem states that if three sides of one triangle are congruent to three sides of another triangle, then the triangles are congruent.
Side-Angle-Side (SAS) Congruence Theorem
The SAS Congruence Theorem states that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent.
Angle-Side-Angle (ASA) Congruence Theorem, Triangles congruence proofs booklet answer key
The ASA Congruence Theorem states that if two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent.
Congruent Triangle Proofs
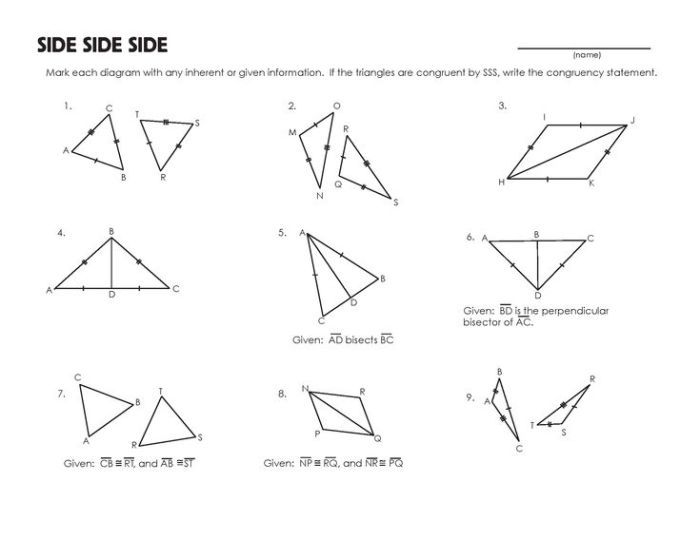
SSS Congruence Theorem Proof
- Given: Triangle ABC and Triangle DEF with AB = DE, BC = EF, and AC = DF.
- To Prove: Triangle ABC is congruent to Triangle DEF.
- Proof: By the SSS Congruence Theorem, since the three sides of Triangle ABC are congruent to the three sides of Triangle DEF, Triangle ABC is congruent to Triangle DEF.
SAS Congruence Theorem Proof
- Given: Triangle ABC and Triangle DEF with AB = DE, BC = EF, and ∠B = ∠E.
- To Prove: Triangle ABC is congruent to Triangle DEF.
- Proof: By the SAS Congruence Theorem, since two sides and the included angle of Triangle ABC are congruent to two sides and the included angle of Triangle DEF, Triangle ABC is congruent to Triangle DEF.
ASA Congruence Theorem Proof
- Given: Triangle ABC and Triangle DEF with ∠A = ∠D, ∠B = ∠E, and BC = EF.
- To Prove: Triangle ABC is congruent to Triangle DEF.
- Proof: By the ASA Congruence Theorem, since two angles and the included side of Triangle ABC are congruent to two angles and the included side of Triangle DEF, Triangle ABC is congruent to Triangle DEF.
Triangle Congruence Proofs Booklet: Triangles Congruence Proofs Booklet Answer Key
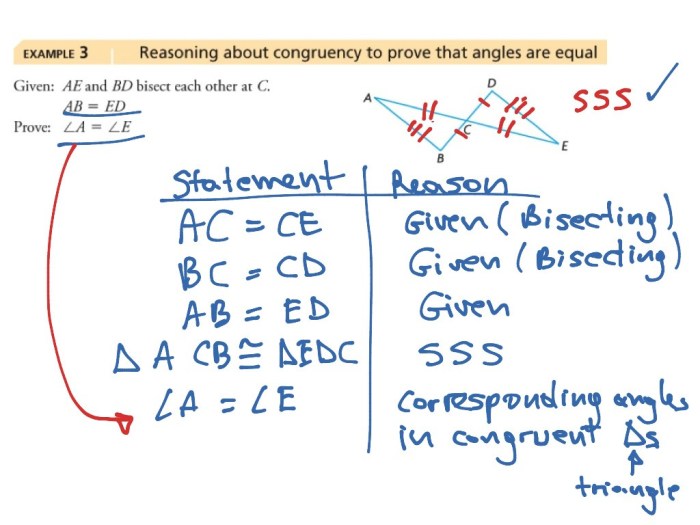
Table of Contents
- Introduction to Triangle Congruence
- Congruence Theorems
- Congruent Triangle Proofs
- Triangle Congruence Proofs Booklet Answer Key
Layout
The booklet will be divided into four sections: Introduction, Congruence Theorems, Congruent Triangle Proofs, and Answer Key. Each section will be further divided into subsections.
Answer Key for Triangle Congruence Proofs Booklet
SSS Congruence Theorem Proof
- Given: Triangle ABC and Triangle DEF with AB = DE, BC = EF, and AC = DF.
- To Prove: Triangle ABC is congruent to Triangle DEF.
- Proof: By the SSS Congruence Theorem, since the three sides of Triangle ABC are congruent to the three sides of Triangle DEF, Triangle ABC is congruent to Triangle DEF.
SAS Congruence Theorem Proof
- Given: Triangle ABC and Triangle DEF with AB = DE, BC = EF, and ∠B = ∠E.
- To Prove: Triangle ABC is congruent to Triangle DEF.
- Proof: By the SAS Congruence Theorem, since two sides and the included angle of Triangle ABC are congruent to two sides and the included angle of Triangle DEF, Triangle ABC is congruent to Triangle DEF.
ASA Congruence Theorem Proof
- Given: Triangle ABC and Triangle DEF with ∠A = ∠D, ∠B = ∠E, and BC = EF.
- To Prove: Triangle ABC is congruent to Triangle DEF.
- Proof: By the ASA Congruence Theorem, since two angles and the included side of Triangle ABC are congruent to two angles and the included side of Triangle DEF, Triangle ABC is congruent to Triangle DEF.
Questions Often Asked
What is the Side-Side-Side (SSS) Congruence Theorem?
The SSS Congruence Theorem states that if the three sides of one triangle are equal to the three sides of another triangle, then the two triangles are congruent.
How do you prove triangles congruent using the SAS Congruence Theorem?
To prove triangles congruent using the SAS Congruence Theorem, you must show that two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle.