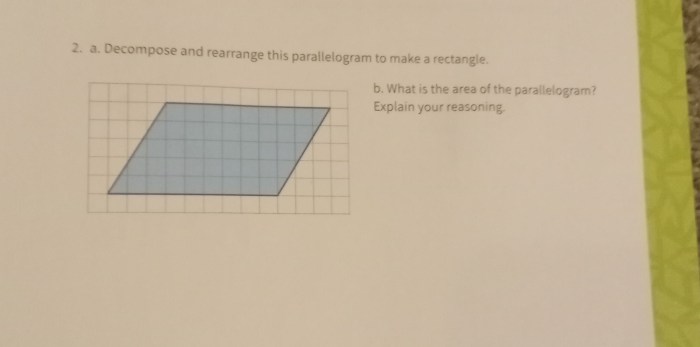
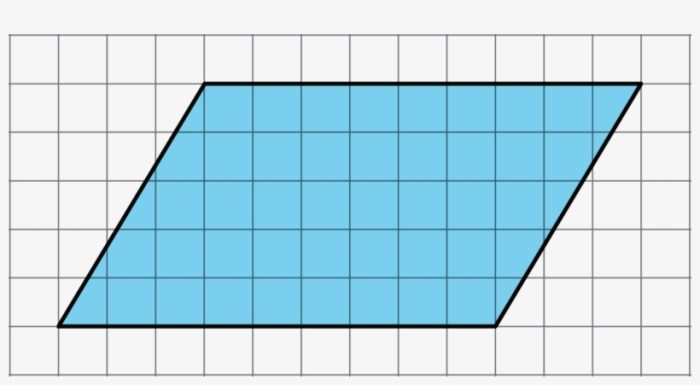
Decompose and rearrange this parallelogram to make a rectangle – Decomposing and rearranging parallelograms to form rectangles is a fundamental geometric concept with practical applications in various fields. This article delves into the process, exploring the properties of parallelograms and rectangles, comparing their similarities and differences, and discussing the significance of this transformation in real-world scenarios.

By understanding the techniques involved in decomposing and rearranging parallelograms, individuals can enhance their spatial reasoning skills, develop a deeper understanding of geometric relationships, and appreciate the versatility of geometric shapes in problem-solving.

Decomposing and Rearranging Parallelograms to Form Rectangles: Decompose And Rearrange This Parallelogram To Make A Rectangle

Parallelograms and rectangles are quadrilaterals with distinct properties and relationships. Understanding how to decompose a parallelogram into its component parts and rearrange them to form a rectangle is a fundamental concept in geometry.

Decomposing a Parallelogram, Decompose and rearrange this parallelogram to make a rectangle

A parallelogram is a quadrilateral with opposite sides parallel and equal in length. To decompose a parallelogram, it can be divided into two congruent triangles.

• Step 1:Draw a diagonal line connecting two opposite vertices.
• Step 2:The diagonal line divides the parallelogram into two congruent triangles.

Rearranging into a Rectangle

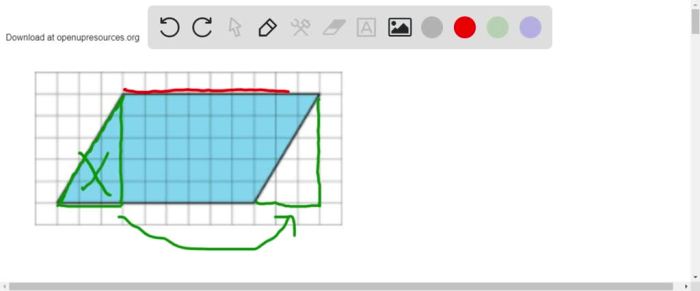
A rectangle is a quadrilateral with four right angles and opposite sides parallel and equal in length. To rearrange the parts of a parallelogram to form a rectangle, one of the triangles obtained from decomposing the parallelogram is flipped and attached to the other triangle.

• Step 1:Decompose the parallelogram into two congruent triangles.
• Step 2:Flip one of the triangles over.
• Step 3:Attach the flipped triangle to the other triangle along the diagonal line.

Comparison of Parallelogram and Rectangle

FAQ

What is the difference between a parallelogram and a rectangle?

A parallelogram has two pairs of parallel sides, while a rectangle has four right angles in addition to having two pairs of parallel sides.

How can I decompose a parallelogram into its component parts?

A parallelogram can be decomposed into two congruent triangles by drawing a diagonal from one vertex to the opposite vertex.

What are the steps involved in rearranging the parts of a parallelogram to form a rectangle?

To rearrange the parts of a parallelogram to form a rectangle, one can cut the parallelogram along a diagonal and then rearrange the triangles to form a rectangle.

You May Also Like

Lesson 1.1 Building Blocks Of Geometry Answer Key

Triangles Congruence Proofs Booklet Answer Key