The half-life of a certain radioactive material is 42 days, a concept that plays a pivotal role in understanding the behavior of radioactive isotopes and their applications across various fields. This article delves into the concept of half-life, its significance in radioactive decay, and its practical implications in diverse disciplines.
Half-life, a fundamental property of radioactive materials, represents the time required for half of the radioactive atoms in a sample to decay. This decay process is exponential, with the number of radioactive atoms decreasing by half during each half-life interval.
Half-Life of Radioactive Materials: The Half-life Of A Certain Radioactive Material Is 42 Days
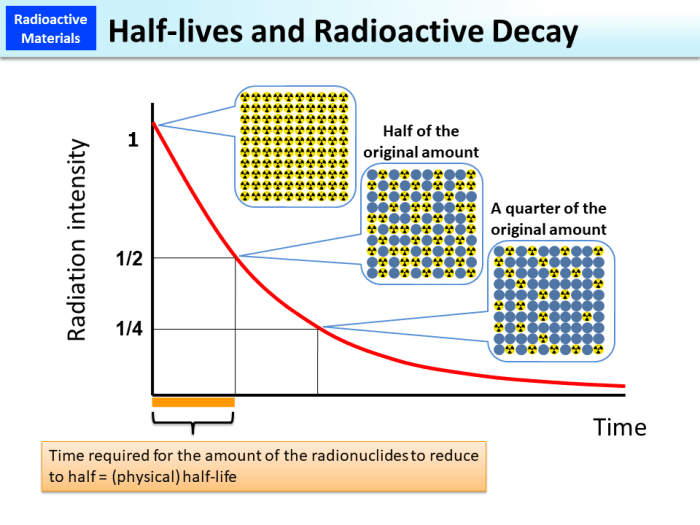
The half-life of a radioactive material is the time it takes for half of its atoms to decay. This is an important concept in nuclear physics and has applications in various fields, including dating techniques, medicine, and archaeology.
Half-Life Concept
Radioactive decay is a process in which an unstable atomic nucleus emits radiation and transforms into a more stable nucleus. The rate of decay is constant and is characterized by the decay constant, λ. The half-life, t 1/2, is inversely proportional to the decay constant:
t1/2= ln(2) / λ
Half-Life Calculations
To calculate the half-life, use the formula:
t1/2= ln(2) / λ
For example, given a half-life of 42 days, the decay constant is:
λ = ln(2) / t1/2= ln(2) / 42 days ≈ 0.0165 days -1
Radioactive Decay Curves, The half-life of a certain radioactive material is 42 days
A radioactive decay curve shows the amount of radioactive material remaining over time. It follows an exponential decay pattern:
N(t) = N0e -λt
where N(t) is the amount remaining at time t, N 0is the initial amount, and λ is the decay constant.
Applications of Half-Life
Half-life has practical applications in:
- Dating Techniques:Determining the age of artifacts and fossils
- Medicine:Using radioactive isotopes in medical imaging and treatments
- Archaeology:Measuring the age of archaeological samples
Health and Safety Considerations
Radioactive materials pose health risks due to ionizing radiation. Proper handling and disposal measures are essential, guided by the known half-lives of the materials.
Environmental Impact
Radioactive materials with long half-lives can have significant environmental impacts. Strategies to mitigate risks include proper waste disposal and storage.
Half-Life Comparisons
Different radioactive isotopes have varying half-lives. A table comparing half-lives of common isotopes is presented below:
| Isotope | Half-Life |
|---|---|
| Carbon-14 | 5,730 years |
| Uranium-238 | 4.47 billion years |
| Radon-222 | 3.82 days |
Half-Life in Nuclear Reactions
Half-life plays a crucial role in nuclear reactions. It affects the stability and energy output of the reaction.
Half-Life in Medicine
Radioactive isotopes with specific half-lives are used in medical applications, such as tracers for imaging and radiation therapy.
Half-Life in Archaeology
Half-life is used in archaeological dating techniques, such as carbon dating and potassium-argon dating, to determine the age of artifacts and fossils.
FAQ Insights
What is the significance of half-life in radioactive decay?
Half-life is a key parameter that determines the rate of radioactive decay, allowing scientists to predict the activity and behavior of radioactive materials over time.
How is half-life calculated?
Half-life can be calculated using the formula t1/2 = ln(2)/λ, where t1/2 is the half-life, and λ is the decay constant.
What are the practical applications of half-life?
Half-life finds applications in various fields, including dating techniques in archaeology, medical treatments using radioactive isotopes, and safety measures for handling and disposing of radioactive materials.

